如何通俗易懂地理解红黑树

红黑树想必大家都不陌生，但是很多同学对它忌讳地很。在他们的刻板印象中，红黑树的红黑规则就是凭空出现的，毫无依据可言。这篇文章的目的就是打破这种刻板印象，让大家知其然也知其所以然。

1. 2-3-4 树

在讲红黑树之前，有必要给大家介绍一下 2-3-4 树，2-3-4 树是理解红黑树的关键。那什么是 2-3-4 树呢？如下图所示，首先 2-3-4 树是一棵查找树；其次 2-3-4 树允许 2-结点，3-结点和 4-结点的存在，这也是 2-3-4 树名字的由来。所谓 2-结点就是最多能有 2 个孩子的结点，3-结点就是最多能有 3 个孩子的结点，依此类推…

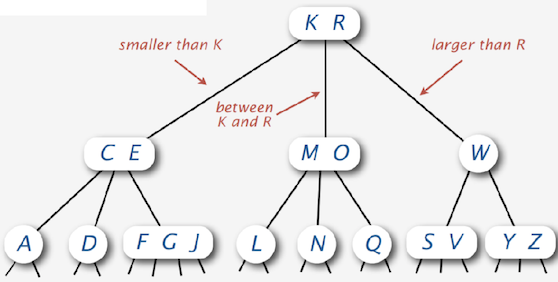
2-3-4 tree

2-3-4 树有一个很酷的性质：在动态地添加和删除元素的时候，只要花费很小的代价就能够保持树的完美平衡。啥叫完美平衡呢？完美平衡指的是，每一条从根结点到叶子结点的路径都是一样长的。直观一点讲，就是所有的叶子结点都位于同一层上。接下来，我们就以 2-3-4 树的插入为例，讲讲 2-3-4 树如何在动态添加元素的过程中保持树的完美平衡。

1.1 插入

就以上图为例，假设我们已经有了一棵完美平衡的 2-3-4 树 (这样的假设是很合理的，因为空树和只有一个元素的 2-3-4 树都是完美平衡的)。现在我们要插入一个元素，首先我们会根据元素之间的大小关系，找到元素要插入的位置。根据插入位置的不同，我们可以分为三种情况：

在 2-结点的位置插入，我们只需要将 2-结点转换成 3-结点即可。

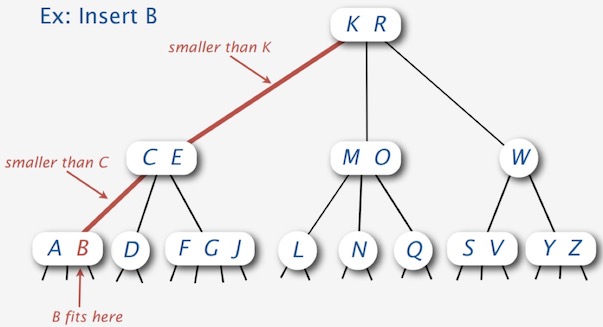
insert-2-node

在 3-结点的位置插入，我们只需要将 3-结点转换成 4-结点即可。
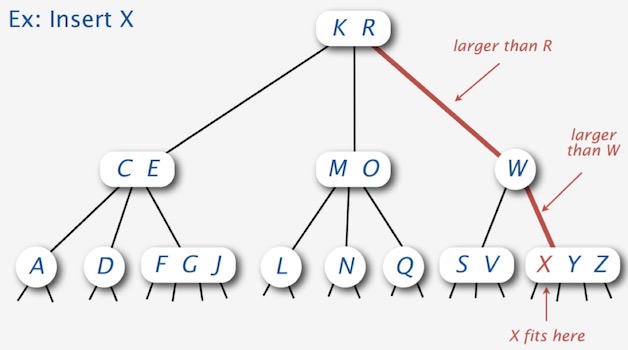
比较麻烦的是，如果我们在 4-结点的位置插入元素，该怎么办呢？

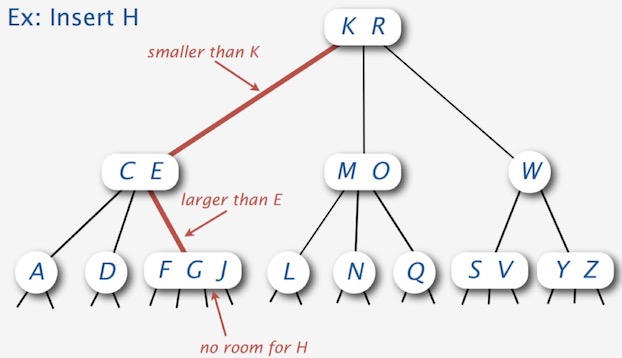
答案是：我们需要将 4-结点进行分裂，以腾出空间给新添加的元素，这样我们就可以像在 2-结点中一样添加元素了。具体过程如下图所示：

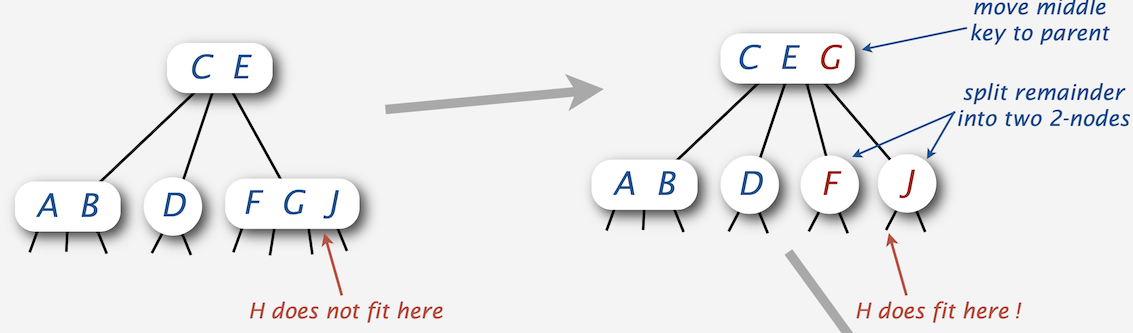
不过这里存在一个小问题，那就是如果父结点也是 4-结点该怎么办呢？这样我们就没办法将中间元素直接添加到父结点中了。处理这个问题主要有两种方式：
- 自底向上：我们以同样的方式分裂父结点，如有必要，我们沿着树一直向上分裂。
- 自顶向下：在查找插入位置的时候，遇到 4-结点就直接分裂，这样就可以保证插入元素的结点不是 4-结点。

1.2 生长过程

接下来，我们就以一个具体的例子来看看 2-3-4 树是如何在动态地添加元素的过程中保持树的完美平衡的，这里我们采用自顶向下的方式分裂 4-结点。

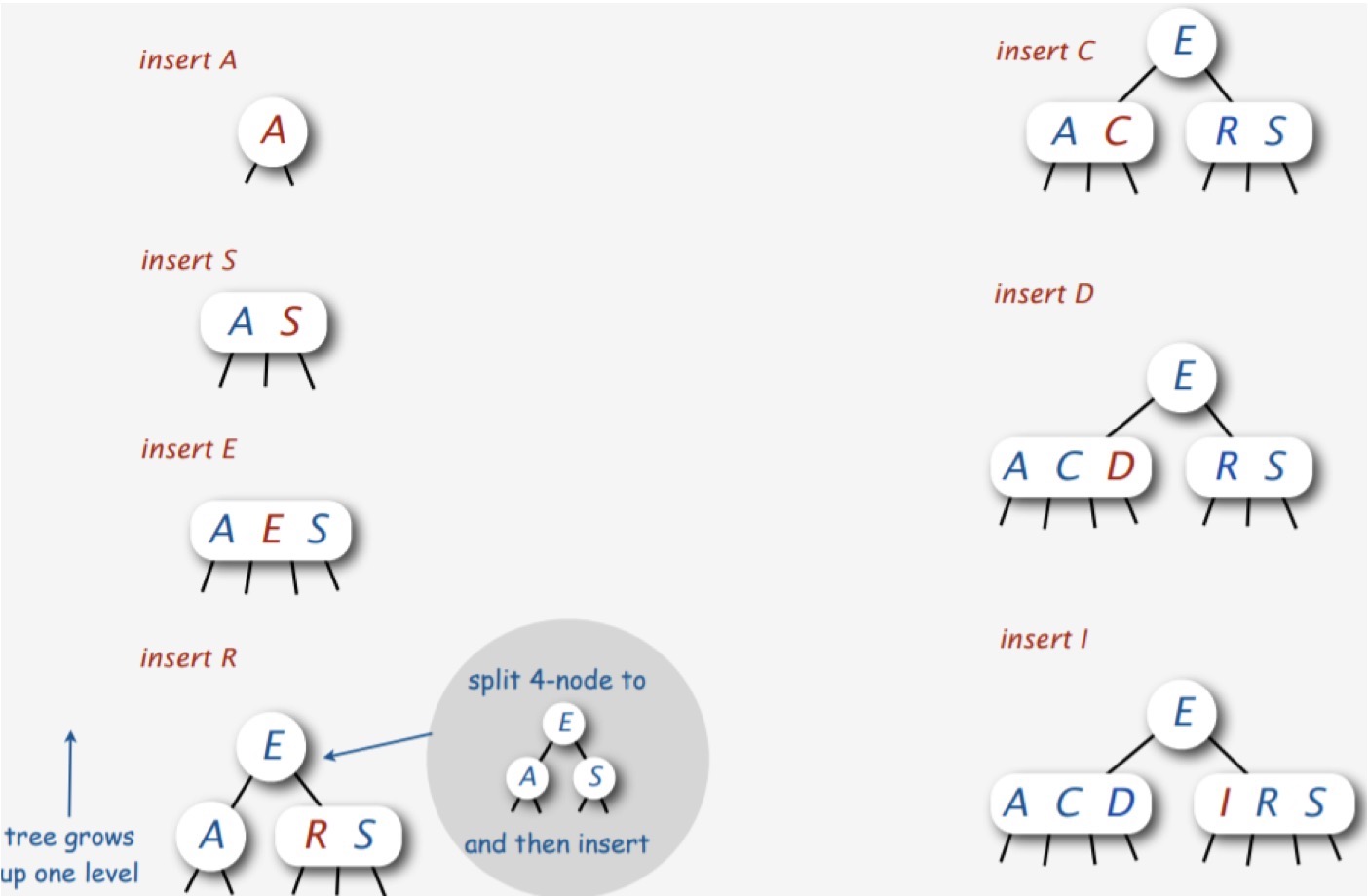
growth-of-tree-1

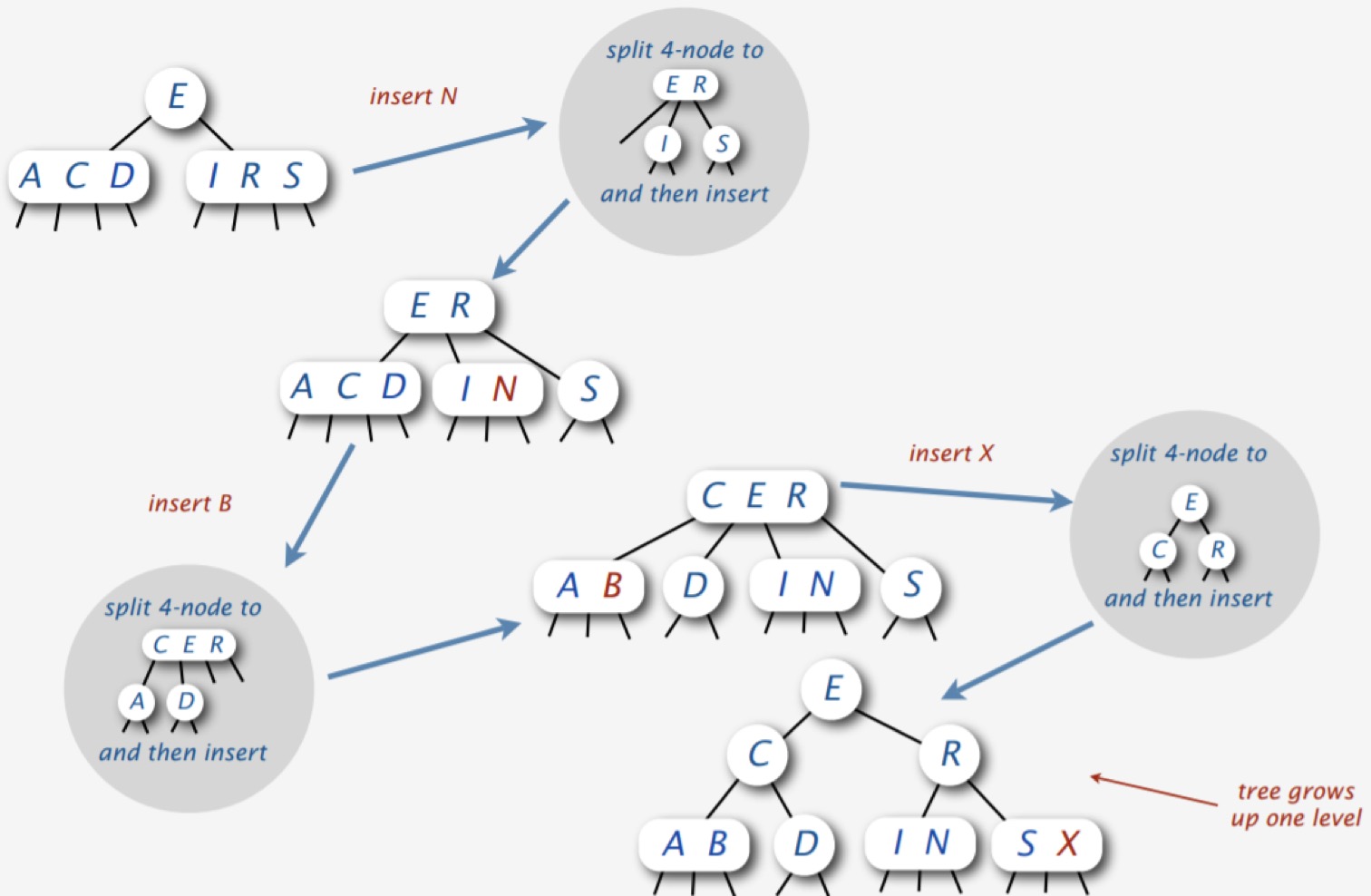
growth-of-tree-2

1.3 性能分析

通过上面的例子，相信你对 2-3-4 树是如何保持完美平衡的有了一定的认识了。那么接下来，我们就来分析下 2-3-4 树的性能。由于 2-3-4 树是完美平衡的，那么最坏情况下，树的高度为 $\log_{2}N$ (所有结点都为 2-节点)；最好情况下，树的高度为 $\log_{4}N$ = $\frac{1}{2}\log_{2}N$ (所有结点都为 4-结点)。我们可以通过一些数据更直观地感受下它的性能：100 万个元素，树的高度在 10～20 之间；10 亿个元素，树的高度在 15～30 之间。

2-3-4 树的高度为 O(lg n)，因此搜索的时间复杂度为 O(lg n)；在添加元素和删除元素时，我们需要做些额外的操作来保持树的完美平衡，这主要是通过树的旋转操作来完成的，可以证明这些旋转操作最多为 O(lg n)，因此添加和删除的时间复杂度也为 O(lg n)。

总体来说，2-3-4 树的性能是非常不错的，搜索、添加、删除的时间复杂度都为 O(lg n)。那么我们又该如何实现 2-3-4 树呢？

1.4 直接实现?

最容易想到的方式就是：编写不同的结点类型分别代表 2-结点，3-结点和 4-结点。这样确实也能够实现，但是会带来许多麻烦：需要管理不同的结点类型；不同的结点类型之间需要相互转换；不好统一 cases。我们可以通过一段伪代码来直观地感受下这种实现方式的复杂度…

private Node insert(K key, V value) {
  	Node x = root;
  	while (x.getTheCorrectChild(key) != null) {
      	x = x.getTheCorrectChild(key);
      	if (x.is4Node()) x.split();
    }
  	if (x.is2Node()) x.make3Node(key, value);
  	else if (x.is3Node()) x.make4Node(key, value);
  	return x;
}

所以，我们期待一种更简单的实现！

2. 红黑树

红黑树就是一种更简单的实现方式，红黑树的核心思想就是用 BST 来表示 2-3-4 树。但是 2-3-4 树有 2-结点、3-结点和 4-结点，而 BST 只有 2-结点，那我们该如何表示 3-结点和 4-结点呢？红黑树使用内部的"红色边"来表示 3-结点和 4-结点。如下图所示：

3-or-4-node

用红色边相连的我们认为是在 2-3-4 树同一个结点内。3-结点有两种表示方式，红色边可以左倾，也可以右倾；4-结点只有一种表示方式，两条红色边必须位于两边，不能位于同一侧。

但是在实现的时候，我们该如何表示这些内部的"红色边"呢？红黑树采用了一种巧妙的方式：在每个结点中添加了一个"红/黑"属性，如果该结点是"红"的，那么就表示该结点与父结点的边是"红"的。

OK，这就是红黑树，简单吧～

接下来，我们就用这样一种"新"的眼光重新来看下红黑树的正式定义：

A red-black tree is a binary tree that satisfies the following red-black properties:

Every node is either red or black.

The root is black.

Every leaf (NIL) is black.

If a node is red, then both its children are black.

For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

以上定义摘自 Introduction To Algorithms。前 3 点没什么好说的；第 4 点其实说的是，不能有两条连续的红色边，因为 4-结点的两条红色边必须位于两侧，不能位于同一边；第 5 点其实就是在说 2-3-4 树是完美平衡的。

重新审视之后，我们会发现红黑树模型其实真的很简单，完全没必要去死记硬背那些红黑性质。

2.1 左倾红黑树

经典的红黑树 3-结点有两种不能的表示方式，红色边可以左倾，也可以右倾，因此红黑树与 2-3-4 树之间不是一对一的关系，如下图所示：

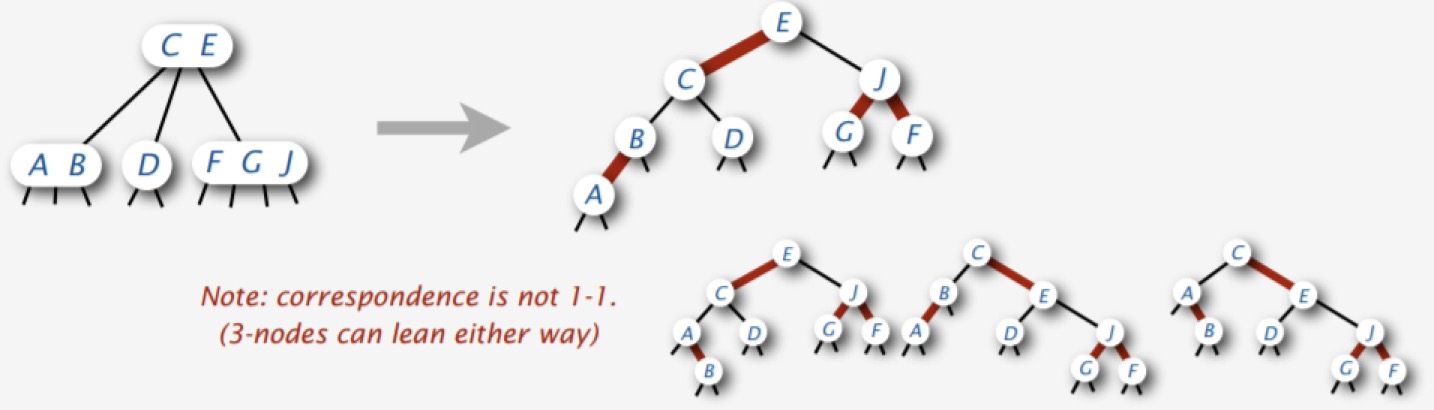
not-1-to-1-correspondence

如果我们在红黑树的基础上，要求 3-结点的红色边必须左倾，那么红黑树与 2-3-4 树之间就是一对一的关系，如下图所示：

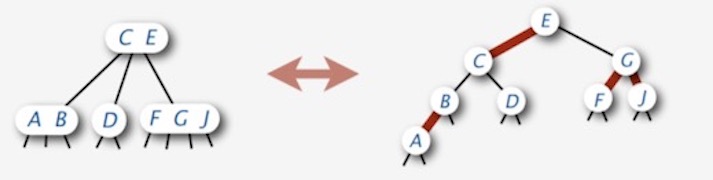
1-to-1-correspondence

这样一种新的红黑树模型，我们称之为左倾红黑树 (Left-leaning Red-Black Tree, LLRB)。

小结

这篇文章主要是让大家理解红黑树模型，因此没有涉及红黑树的实现。对经典红黑树实现感兴趣的同学，可以参考 Introduction To Algorithms 和 jdk TreeMap 的源码。对左倾红黑树实现感兴趣的同学，可以参考 Robert Sedgewick 的 Algorithms 以及这本书的配套网站。